3.重力による運動
地球上の物体には地球からの引力による鉛直下向きの力が常にはたらいている。この力を重力といい、質量mの物体にはたらく重力はm![]() である。ここで、
である。ここで、![]() は重力加速度とよばれ、その値は地球上でほぼ一定で9.8m/s2である。また、物体が受ける重力の大きさが物体の重さである。すなわち、物体の重さは力であって質量とは異なるので注意が必要である。質量1kgの物体は地球上では9.8Nの重力をうける。従って、質量1kgの物体の重さは9.8Nであり、これを1kgw(キログラム重)とよぶこともある。
は重力加速度とよばれ、その値は地球上でほぼ一定で9.8m/s2である。また、物体が受ける重力の大きさが物体の重さである。すなわち、物体の重さは力であって質量とは異なるので注意が必要である。質量1kgの物体は地球上では9.8Nの重力をうける。従って、質量1kgの物体の重さは9.8Nであり、これを1kgw(キログラム重)とよぶこともある。
地球上では物体には常に鉛直下向きに重力がはたらく。地上での物体の運動では、空気抵抗を無視すると、物体に作用する力はこの重力のみである。すなわち、重力が地上での物体の運動の原因である。地球上では物体はその重さに関係なく、一定の加速度で落下する。この加速度が重力加速度である。
3.1 自由落下運動
物体をある高さから初速度0で落下させたときの物体の運動を自由落下運動という。
| 自由落下運動は一次元の運動である。そこで、物体の落下方向に落下距離のz軸をとり、時刻tにおける物体の落下位置をz(t)とし、そのときの物体の速度をv(t)する。すると、この場合の(Newtonの)運動方程式は物体の質量をmとして、 である。また速度v(t)を用いると、(Newtonの)運動方程式は となる。そして物体の始めの位置を原点にとると、初期条件はv(0)=0、z(0)=0である。 また、両辺のmを消去して、 となる。式(3)は物体の落下の加速度が質量mに関係なく そして、両辺を時間tで積分すると、 より、 v(t)= である。そして、初期条件よりC1=0であるので、この場合 v(t)= となる。さらに、式(4)は落下位置z(t)の時間微分を用いて、 と表されるので、両辺を時間tで積分して、 より、 さらに初期条件より、C2=0である。従って、t秒後の物体の落下位置z(t)は である。すなわち、落下距離は時間の自乗に比例する。 次に、質量mの物体を高さhから初速v0で真上に投げ上げたときの運動について考える。今度は鉛直上向きに物体の位置を表すz軸をとると、(Newtonの)運動方程式は となる。そして初期条件はv(0)=v0、z(0)=hである。式(6)を与えられた初期条件のもとで解くことにより物体の速度と位置を求めることができる。この場合、速度は v(t)=− となり、位置は となる。さらに、式(7)から、物体が最高点に達する時刻t0はv(t0)=0より、 t0=v0/ であり、その高さは である。 |
|
 |
|
3.2 放物運動
| 質量mの物体をある高さから水平に初速度v0で投げ出したときの、物体の運動について考える。この場合の運動は二次元の運動で、水平方向にx軸、鉛直下向きにy軸をとる。物体に作用する力は鉛直下向きの重力だけなので、この場合の(Newtonの)運動方程式は | |
となる。従って、水平方向には等速度運動、鉛直方向には自由落下運動をする。 そして初期条件はそれぞれ、 vx(0)=v0 、vy(0)=0 x(0)=0 、 y(0)=0 である。まず、水平方向の運動について考える。式(10)の両辺を時間tで積分して、 である。そしてここで、初期条件より、Cx1=v0であるので、水平方向の速度は vx(t)=v0 である。また、時刻tにおける物体の水平位置x(t)は、初期条件x(0)=0より、 x(t)=v0t である。次に鉛直方向の運動は、自由落下運動であるので、速度と位置は初期条件より、 vy(t)= となる。また、任意の時刻における物体の速度vは、速度の合成より、 v=vx+vy で、その大きさは である。 |
|
|
次に、質量mの物体を水平から上向きに角度θ、初速度v0で投げ出した場合の放物運動について考える。この場合にも物体に作用する力は鉛直下向きの重力のみである。水平方向にx軸、鉛直方向にy軸を取ると、この場合の(Newtonの)運動方程式も |
|
|
|
|
この場合の運動の軌跡(x(t),y(t))は、これらの式から時間tを消去して、 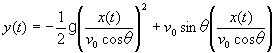 である。これを整理して、 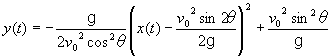 となる。従って、放物運動の軌跡は、 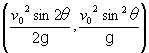 を頂点とする二次曲線である。この軌跡は別に放物線とも呼ばれる。放物運動の頂点の座標から物体は、最高点が を頂点とする二次曲線である。この軌跡は別に放物線とも呼ばれる。放物運動の頂点の座標から物体は、最高点が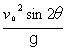 となり、空気抵抗が無視できる場合には物体を45°の角度で投げ出すと最も遠くまで飛ぶことがわかる。 となり、空気抵抗が無視できる場合には物体を45°の角度で投げ出すと最も遠くまで飛ぶことがわかる。 |
|
3.3 空気抵抗を考慮した場合の自由落下運動
|
これまで、質量mの物体に作用する力が重力のみの運動を考えてきたが、空気中を運動している物体には重力の外に空気抵抗がはたらく。空気抵抗は物体の速度vに比例し、その運動を阻止する向きに作用する。すなわち、速度vの物体の受ける空気抵抗は−kvと表される。そこで、鉛直方向下向きにz軸をとり、時刻tにおける速度をv(t)とすると、この場合の運動方程式は、 |
|
|
そして、初期条件はv(0)=0、z(0)=0である。 |
|
| 終端速度では空気抵抗と重力がつり合うため物体は等速度運動をする。地表近くでの雨粒は終端速度に達しているため等速度で落下する。 | |