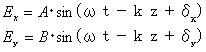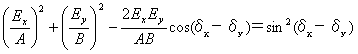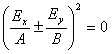|
| |
| 目的 |
| 偏光の関係するさまざまな現象を観察し、偏光に関する基礎的理解を得る。 |
| |
偏光とは
波はその変位の方向と波の進行方向の関係から、縦波(longitudinal
wave)と横波(transversal
wave)とに分けられる。縦波は変位の方向が波の進行方向と平行な波で、音波がその代表例である。一方、横波はその変位が進行方向に垂直な波で、縦波とは違い変位の方向に自由度がある。この自由度のなかで、変位の特定の方向への振動を偏りという。 |
| 参照 実験 1)偏光板のはたらき |
| |
光りは横波である電磁波(electromagnetic wave)の一種で、我々が可視光と呼ぶのは波長0.4μm〜0.7μmの電磁波である。光を波として捉えるとき、その振幅Aの自乗(A・A*)が光の強度である。
光は横波であるので、"偏り"を示す。これを偏光(polarized light)という。光の偏光状態は、光の電気ベクトルの先端が描く軌跡として定義される。光の伝播方向に垂直な面内で、電気ベクトルの先端が直線を描く場合、その光は直線偏光(linearly
polarized light)と呼ばれ、電気ベクトルの先端が円を描く場合は円偏光(circularly
polarized light)と呼ばれる。そして、電気ベクトルの先端が楕円を描く場合、それは楕円偏光(elliptically
polarized light)と呼ばれる。光の偏光状態は直交した二つの直線偏光の"重ね合わせ"として理解することもできる。(図1) |
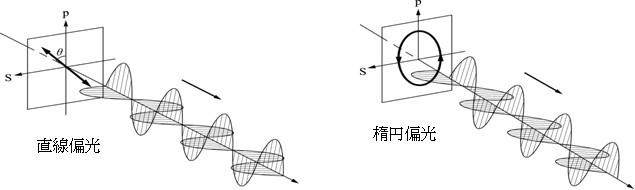 |
| 図 1 |
| いま、波の進行方向をz軸とし、それに垂直な平面上に直交するxとy軸をとる。そして、光の電気ベクトルのx成分とy成分をそれぞれ、 |
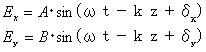 |
|
(1) |
| とすると、この光の電気ベクトルが描く軌跡は、上式より、sin(ωt−kz)を消去して |
| |
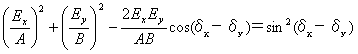 |
(2) |
| となる。ここで、式(2)は一般に楕円をあらわす式である。すなわち、振幅が異なり、互いに直交して振動する二つの直線偏光(ExとEy)を、位相をずらして重ね合わせると、その合成した光は楕円偏光となることを示している。そして、δx−δy=0、またはδx−δy=πのとき、式(2)は |
| |
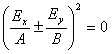 |
|
(2.1) |
となり、直線の式 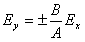 となる。これは直線偏光を表わす。 となる。これは直線偏光を表わす。
また、A=Bでかつ、δx−δy=±π/2のとき、式(2)は |
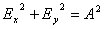 |
|
(2.2) |
| となり、円の方程式となる。すなわち、この場合、円偏光となる。位相差の±はそれぞれ、左回りと右回りの円偏光に対応している。 |