光が界面で反射される際、反射光では一般に、振幅（amplitude）の変化と位相（phase）の跳びが生じる。反射の際の振幅反射率（amplitude reflectivity）をｒ、位相の跳びをδとすると、ｒ･exp(ｉδ)を複素振幅反射率という。複素振幅反射率の値は、光の入射角と界面の屈折率（refractive index）で決まってくる。
さらに、複素振幅反射率は入射する光の偏光状態（polarization state）にも依存する。図２に示すように、電気ベクトルが入射面内で振動する光の成分をｐ成分（ｐ偏光）と呼び、電気ベクトルが入射面に垂直に振動する光の成分をｓ成分（ｓ偏光）と呼ぶが、これら、ｐ、ｓ偏光に対する界面の(複素)振幅反射率を与える式がフレネル係数（Fresnelcoefficient）である。 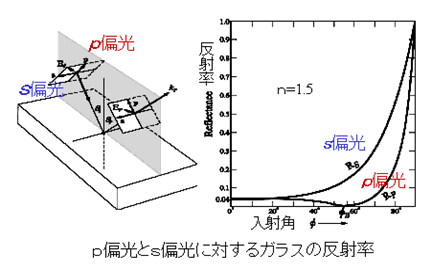図 2
以下に、空気中から屈折率ｎの透明媒質に入射角φで光が入射するときのフレネル係数の式を示す。
		(3)
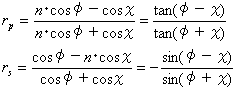
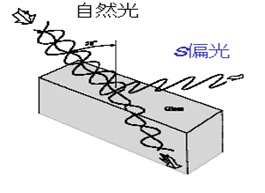
ここで、sinφ = n･sinχ（Snell's law：スネルの法則）である。反射面が水やガラスのように透明な物質の場合、フレネル係数（複素振幅反射率）は実数となるので、δ＝０またはπである。 そして、強度反射率（Ｒp､s＝ｒp､s２）を図示したものが図２(右)である。図２から、ｐ偏光では、ある入射角で反射率が０となることがわかる。この入射角をブリュ−スター角（Brewster's angle）または偏光角（polarization angle）という。屈折率ｎの媒質に対するブリュ−スター角をφＢとすると、ｐ偏光に対するフレネル係数の式より、 　 tanφB＝ｎ が成り立つ。 　また、図２からわかるように、ｓ偏光の方がｐ偏光より反射率が大きいので、界面からの反射光は一般にｓ成分を多く含む光となる。そして、ｐおよびｓ成分を含む光が、Brewster角でガラス表面に入射すると、反射光は図３に示すように、完全にｓ偏光（ｓ成分のみ）となる。図４-１では雨上がりの濡れた路面に人の像が映っているが、これをｐ方位の偏光子を通して見ると、水面からの反射である人の像は消えてしまう（図４-２）。
参照　実験　3)偏光の反射とBrewster角(1)
参照　実験　3)偏光の反射とBrewster角(2)
図 3 図 4-1 図 4-2